Potek dela

Ugotoviti moramo splošno formulo za izračun obsega n-kotnika. Vemo, da je obseg n-kotnika malo manjši od obsega 2n-kotnika. n-kotnik včrtamo v enotski krog (torej, krog s polmerom 1) in ga razrežemo na n enakostraničnih trikotnikov. Ti trikotniki so sestavljeni iz dveh enako dolgih stranic (polmerov) in iz stranice a. Naj bo kot med polmeroma in naj bo obsek n-kotnika . Podobno lahko razrežemo 2n-kotnik, le da imamo tukaj v trikotnikih polmera in stranico b, kot med polmeroma ter obseg .

Recimo, da poznamo obseg . Potem lahko izračunamo na sledeč način:

Ker velja in izpeljemo

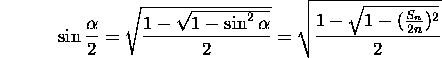
iz česar sledi

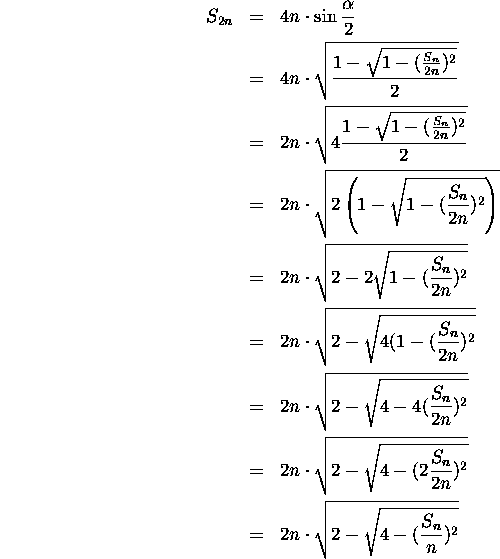
Zatorej, če poznamo poznamo tudi .

Preden bomo napisali program preverimo našo formulo na nekaj primerih:

• V krog včrtamo enakostranični trikotnik in dobimo:

  

• Izračunajmo še obseg kvadrata, ki smo ga včrtali v enotski krog:

  

Napišimo program!:

#include <stdio.h>
#include <conio.h>
#include <math.h>

#define sqr(x) x*x

#define DVA_PI 6.2831854

void main() {
  float s;
  int n;

  clrscr();

  n= 3;            /* zacetni priblizek je pravilni 3-kotnik */
  s= 3*sqrt(3);
  do {
    s= sqrt(2-sqrt(4-sqr(s/n)));
    n= 2*n;                      /* n=2n */
    s*= n;
    printf("Obseg %d-kotnik je %f, resnicni PI=%f\n", n, s, DVA_PI);
  } while(getch()==`d`);
} /* main */

Začetni približek lahko dobimo tudi na drugačen način. Vzamemo pravilni 2-kotnik, ki je premer kroga in dobimo:

Torej

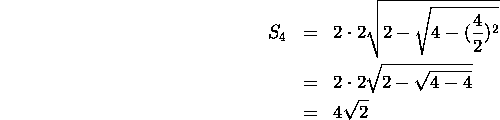
Kar je pravilno.